Trækkraft - og andre kræfter
af Flemming Lund, DMJK (først offentliggjort i Signalposten nr. 5, 1975)
Efter de første prøvekørsler og indvielsen af det nye anlæg på Gb, er jeg blevet spurgt om det var muligt på forhånd at sige noget om, hvor stor trækkraft et givet loko kan forventes at præstere. Emnet har interesseret mig længe, så i det efterfølgende vil jeg forsøge at give en oversigt over de fysiske forhold, der spiller ind, ligesom jeg vil, ud fra disse forhold, prøve at opstille nogle generelle regler, der kan anvendes ved bygning af modeller, såvel loko som vogne. Det er klart, at sådanne betragtninger må blive meget generelle og derfor må tages med alle mulige forbehold; men et fingerpeg kan de fundne tal vel altid give. Men lad mig kaste os ud i nogle lange udredninger, som jeg håber at kunne gøre nogenlunde forståelige, og begynde med:
1) Virkelige vægte og modelvægte
Vore modeller bygger vi jo i skala 1:45 med hensyn til mål, men med hensyn til vægtene stiller det sig noget anderledes. Skulle vægtene også være modeltro, vil 1 tons virkelig vægt svare til ca. 11 g i skala 1:45, idet den virkelige vægt skal reduceres med 45 i tredie potens, da det er alle tre dimensioner, nemlig både længde, bredde og højde, der skal reduceres.
En personvogn litra A vejer tom ca. 32 tons, det skulle så give en modelvægt på 32 * 11 = 352 g. I gennemsnit vil jeg regne med at en model af A-vognen vil veje ca. det dobbelte. Ser vi på en MZ, der har træk på alle seks aksler, vejer den driftsklar ca. 120 tons, svarende til en modelvægt på 120 * 11 = 1320 g. Går vi stadig ud fra A-vognen, skulle MZ-modellen veje ca. 2600 g og stadig have træk på alle seks aksler, for at forholdet er passende. De 2600 g lyder passende for en sådan model, men i praksis vil der alligevel mangle noget med hensyn til trækkraft.
Forklaringen er enkel og ligetil: For det første er det svært at lave træk på alle seks aksler, så de fleste vil nok nøjes med træk på to eller fire aksler. Derved er adhæsionsvægten, der er vægten på de drivende aksler, nedsat, og dermed også trækkraften. For det andet er anlægget vi kører på, af pladsmæssige grunde, bygget med større stigninger end forbilledet, ligesom kurverne, normalt 2 m radius, er mindre end DSB tillader på havnespor. At den gennemsnitlige rullemodstand fra et antal vogne også er større i model end i virkeligheden, vil jeg senere komme tilbage til. Disse forhold i forening gør, at det er nødvendigt, for at kunne køre med noget nær det samme antal vogne på modelanlægget som i virkeligheden, at overdrive trækkraftens vægt så meget som muligt, samtidig med at vognenes vægt holdes så lavt som muligt.
I denne forbindelse vil jeg henvise til klubbens standardblade, som jeg vil anbefale alle, der bygger rullende materiel, at læse grundigt igennem.
"Sammendrag"
Vogne bygges så lette som muligt.
Trækkraft bygges med så stor adhæsionsvægt som muligt.
2) Rullemodstande
For at få nogle tal at sætte på tingene, må vi se på hvor store de kræfter er, der skal til at trække en vogn, eller med andre ord, hvilken rullemodstand en give vogn har. Rullemodstanden kan opdeles i tre dele, nemlig:
- Rullemodstanden på lige bane, vandret.
- Rullemodstanden på lige bane, på stigning.
- Rullemodstanden i vandret liggende kurve.
I praksis må vi jo se på det værste tilfælde, nemlig når alle tre forhold optræder samtidigt, som de gør på anlægget på Gb. De afsluttende eksempler er derfor også et udtryk for dette.
For at finde disse modstande, har jeg benyttet et skråplan, som vist på fig. 1, idet der må være balance mellem kræfterne, når vognen ruller med konstant hastighed ned ad skråplanet. Vognvægten P tænkes at angribe i vognens tyngdepunkt, og den virker altid lodret nedad. Denne opløses i de to dele N og F, henholdsvis vinkelret på og parallelt med skinnelegemet på skråplanet. Ved konstant hastighed er kraften F, der forsøger at trække vognen nedad skråplanet, lige så stor, men modsat rettet, modstanden F', der forsøger at holde vognen tilbage. Det kan kortere udtrykkes ved at sige, at de indre kræfter er i ligevægt.
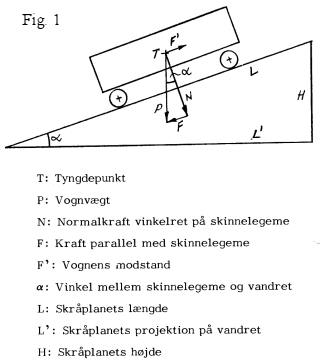
Matematisk findes F = F' af:
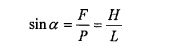
idet trekant PNF er ensvinklet med trekant LL'H.
For at få et generelt mål for rullemodstanden, beregnes denne i gram pr. kg vognvægt og kaldes Q.
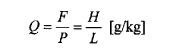
Denne modstand kan deles i to dele, nemlig rullemodstanden mellem hjul og skinne, samt gnidningsmodstanden i lejerne. Den første er næppe målelig ved glatte løbeflader på hjulene, medens den anden har den altafgørende betydning, så den vil vi se nærmere på.
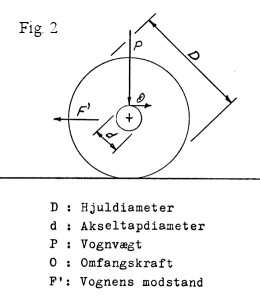
Fig. 2 viser et hjulsæt med akseltap. For at finde et udtryk for modstanden, beregnes det nødvendige arbejde (kraft gange vej) for en bestemt kørelængde, her 1 hjulomdrejning.
Med figurens betegnelser fås, idet det ydre arbejde skal være lig med det indre ved akseltappen, og omfangskraften O = gnidningskoefficienten µ gange vognvægten P.
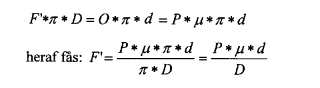
Af denne ligning fremgår det, at jo mindre hjuldiameter D, jo større modstand, og jo større akseltapdiameter d, jo større modstand. Dette bekræftes af de udførte forsøg. Disse faktorer er opført i fig. 5 og 6. Men tilbage til udgangspunktet, nemlig:
2-1: Rullemodstand på lige bane, vandret
Disse forsøg er udført med et hjulsæt efter JS/DMJK standardblad 6, gengivet på fig. 3, med en diameter på 22 mm, svarende til et 1 m hjul. På dette bør man navnlig lægge mærke til løbebanens hældning på 3°, der bevirker at flangen, på lige bane, ikke kommer i berøring med skinnen. Det andet, man bør lægge mærke til, er rundingen mellem løbebane og flange. Denne har stor betydning, som jeg vil prøve at vise i næste afsnit.
Klik for at se >> fig. 3
Her må jeg indskyde en forudsætning eller postulat, om man vil, idet jeg vil hævde, at den smøring med tynd olie, som i mange tilfælde anvendes, kun har begrænset virkning. Endda så begrænset, at ulempen, olie på hjul og spor, er større end virkningen på længere sigt. Olien tørrer nemlig hurtigt ud i et åbent leje, måske allerede på 2-4 uger. I heldigste fald fordamper den bare; i værste fald efterlader den en klæbrig masse, der ikke smører, men klistrer.
| Lejetype | Modstand g/kg |
| Messingleje | 18-22 |
| Messingleje+Molykote | 15-19 |
| Med Teflonbøsning | 12-16 |
| Kugleleje | 6-10 |
| Hjuldiameter mm | Faktor |
| 14 | 1,6 |
| 16 | 1,4 |
| 18 | 1,2 |
| 20 | 1,1 |
| 22 | 1,0 |
| 24 | 0,9 |
| Akseltapdiameter mm | Faktor |
| 1,5 | 0,75 |
| 2,0 | 1,0 |
| 3,0 | 1,5 |
| 4,0 | 2,0 |
| Ved kuglelejer altid | 1,0 |
Af den grund har jeg udført alle forsøgene undtagen et med ikke smurte lejer. Molykote-fedtet jeg har anvendt beholder nemlig sin smøreevne meget længe. Et leje jeg har haft kørende nu i 4 år, har stadig fedt i behold.
Af lejer er undersøgt 4 forskellige, nemlig:
- almindeligt messing- eller bronzeleje,
- samme leje som a), men smurt med Molykote Pasta G Rapid,
- leje med teflonbøsning,
- kugleleje.
I fig. 4 er forsøgenes tendens opstillet, idet forsøgene viste nogen spredning. Jeg mener dog, at disse tal er repræsentative, når der ikke optræder klemning i lejerne, eller andre, uvedkommende ting spiller ind. Disse størrelser er svagt faldende med stigende vognvægt, men kun meget svagt.
Sammenlignes resultaterne med de tal, jeg kan finde for forbilledet, findes her en modstand, der er så lille som 2-3 g/kg vognvægt. Forskellen kan vel kun ligge i forbilledets mere sikre lejring og smøring, som vi ikke har stor mulighed for at efterlave i målestoksforhold.
2-2: Modstand på en stigning
For at udlede denne, vender vi endnu engang tilbage til skråplanet på fig. 1. Hvor vi før lod vognen rulle nedad med jævn hastighed og kaldte modstanden F', vil vi nu prøve at trække den op ad skråplanet. For at gøre dette må rullemodstanden på lige bane overvindes; men herudover må kraften F parallelt med med skinnelegemet, og hidrørende fra vognens vægt, overvindes. Den udledes som tidligere af:

Da vinklen a er meget lille, begår jeg ingen stor fejl ved at sætte L = L', og får derved det lettere håndterlige udtryk:
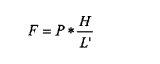
Udtrykket H/L' er, for L' = 1000, det samme som stigningen i promille. Den modstand som skal tillægges rullemodstanden på vandret bane, bliver derfor i gram pr. kg vognvægt = stigningen i promille. Er stigningen for eksempel 10 promille, er modstanden derfor 10 g/kg. Den største stigning på anlægget på Gb er ca. 16 promille, altså en modstand på 16 g/kg vognvægt.
"Sammendrag"
Da stigningen er bestemt af anlæggets udformning, må det blot konstateres, at modstanden er af denne størrelse; det eneste der kan ændres ved er, at holde vognvægten så lav som muligt.
2-3: Rullemodstand i vandret liggende kurve
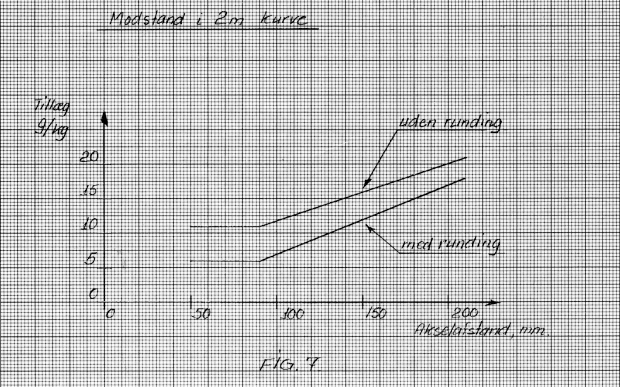
Denne modstand er det ikke muligt for mig at finde matematisk, men kun ved forsøg. Der er dog to ting jeg vil fremhæve. Det ene er, at vi jo næsten altid benytter 2 m kurver af pladshensyn, hvilket svarer til 90 m hos forbilledet. Denne kurveradius ligge faktisk under det mindstemål som DSB anbefaler på havne- og fabriksspor. Populært sagt ligner det noget med eksprestog på havnespor. Det andet er, at i en 2 m kurve kan et standardhjulsæt ikke rulle rundt på løbefladen. Har hjulsættet den på standardblad 6 (fig. 3) viste runding, løber det et stykke op på denne, for at gøre diameterforskellen tilstrækkelig stor.
Mangler rundingen, må hjulsættet "skrabe" sig igennem kurven. På fig. 7 er vist de resultater, jeg er nået frem til ved forsøgene med hjulsæt med og uden den nævnte runding mellem løbebane og flange. Også her gælder det, at der er stor spredning på resultaterne, så disse kurver må også tages med et vist forbehold.
Den aflæste værdi tillægges modstanden for lige bane, vandret. Akselafstanden er afstanden mellem de to yderste aksler på stive vogne. På bogievogne kører bogierne som to, korte, selvstændige vogne, hvorfor det er bogiernes akselafstand, der skal benyttes.
For forbilledet angiver "Hütte", bind III, en empirisk formel efter Röckl:
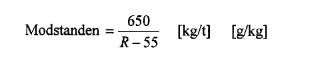
hvori R = kurveradius i m.
Indsættes R = 90 m i denne, fås en modstand på 18,6 kg/t eller g/kg. Det angives at størrelsen er afhængig af akselafstanden, men ikke hvordan. I DSB "Sporregler" optræder samme formel som reduktionsfaktor for nedsættelse af stigningen i kurver i den hensigt at opretholde en konstant modstand. Ud fra disse oplysninger vil jeg gætte på, at formlen henfører til en ret stor akselafstand. Efter min mening burde resultaterne i fig. 7 være større end tilfældet er, sammenlignet med Röckl's formel. En forklaring på forskellen kan jeg dog ikke give på nuværende tidspunkt.
"Sammendrag"
1) Vognvægten bør holdes så lav som muligt.
2) Ved fremstilling af hjul, bør standardblad 6 følges nøje. Især løbebanens hældning og rundingen mellem løbebane og flange bør der ofres opmærksomhed på.
3) Beregning af den samlede rullemodstand
Som tidligere nævnt er det nødvendigt at se på de værste tilfælde, det vil sige lægge alle tre modstande nævnt under 2 sammen. For at gøre dette på en praktisk måde, vil det være en fordel at anvende et skema som vist på fig. 8. I fig. 9, 10, 11 og 12 har jeg forsøgt dels at vise brugen af skemaet, dels at illustrere de forskelle, der kan være på rullemodstanden for den samme type vogn, bygget efter forskellige principper.

Jeg skal endnu en gang gøre opmærksom på, at de tal jeg har fundet frem til i det foregående, kun er og kan blive gennemsnitsværdier, men ikke desto mindre giver de et indtryk af størrelsesordenen, og af de forhold det er muligt at ændre på ved bygning af rullende materiel. Disse muligheder er noteret i slutningen af de enkelte afsnit som "Sammendrag".
Klik for at se >> fig. 9 >> fig. 10 >> fig. 11 >> fig. 12
4) Forventet trækkraft
De tal, der er kommet ud af det foregående, siger jo ikke så meget i sig selv; men sammenholdes de med den trækkraft, det kan forventes et loko kan yde, kan det give mening. Grunden til, at jeg har behandlet rullemodstanden først, er ganske simpelt, at nogle af de ting, der indgår heri, skal benyttes igen her i dette afsnit.
Et lokos trækkraft er afhængig af i hvert fald tre ting:
1) Adhæsionsvægten.
2) Gnidningskoefficienten mellem hjul og skinne.
3) Modstande, bl. a. fra løbeaksler og strømaftagere.
Ad 1: Adhæsionsvægten er den vægt der hviler på de drivende hjul. For at holde denne konstant, er det nødvendigt at eventuelle løbeaksler er fjedrende ophængt, så ujævnheder i sporet ikke får lokoet til at hvile på løbeakslerne i stedet for på drivakslerne. For at holde adhæsionsvægten så stor som mulig, er det nødvendigt at gøre den del af vægten, der hviler på eventuelle løbeaksler så lille som mulig - dog ikke under 125 g pr. aksel.
Ad 2: Gnidningskoefficienten mellem hjul og skinne er defineret som forholdet mellem den lodrette kraft Pa og den vandrette kraft F, der er nødvendig for at få et legeme til at bevæge sig med jævn hastighed hen ad en plan flade. På fig. 13 er dette forhold vist. Ved rimeligt rene hjul og skinner ligger denne størrelse meget nær 0,2. Er der olie eller andet smøremiddel på skinnerne, kan den falde til under halvdelen. Størrelsen µ = 0,2, som jeg vil anvende i de efterfølgende beregninger, optræder, som det fremgår af definitionen, når drivhjulene "spinner" på skinnerne. Kan dette undgås, kan det påregnes at man kan overføre en større kraft, idet det ved forsøg kan påvises, at gnidningskoefficienten ved stilstand µ0
![]()
Dette kan til en hvis grad udnyttes ved at starte lokoet så forsigtigt, at hjulene ikke "spinner" på skinnerne. En hjælp til lettere at opnå dette er at indskyde en centrifugalkobling i lokoets transmission.

Ad 3: Disse modstande er normalt rullemodstande fra eventuelle løbeaksler og tenderaksler, beregnet efter samme princip som brugt i skemaet fig. 8 for vogne, samt modstande, hidrørende fra strømaftagere. Efter vore standards er alle loko forsynet med 2 sæt strømaftagere, hvoraf det halve altid er i funktion. Deres tryk på tredieskinnen nedsætter naturligvis adhæsionsvægten. Strømaftagertrykket er fastsat i standardblad 10 til mellem 30 og 60 g pr. side. Af hensyn til god elektrisk forbindelse mellem strømaftager og tredieskinne, skal trykket være så stort som muligt. Som et passende kompromis mellem disse to modstridende forhold, har jeg valgt at benytte et tryk på 60 g i de følgende beregninger.
Før vi går videre må jeg, for at beregningerne skal blive rigtige, forudsætte, at motoren er så kraftig, at den under alle forhold kan bringe lokoets hjul til at "spinne" på skinnerne. Ligeledes må jeg forudsætte, at eventuelle løbeaksler er ophængt således, at de kan bevæge sig frit i sporet sideværts, samt at deres aksler i kurver indstiller sig tilnærmelsesvist vinkelret på sporets midterlinie. Det vil sige, at enakslede bogier har et omdrejningspunkt, der ligger et stykke væk fra akslen, normalt benævnt Bissel-truck.
For at udføre de nødvendige beregninger mest hensigtsmæssigt, har jeg opstillet det i fig. 14 viste skema. Til skemaet skal knyttes nogle få kommentarer, idet jeg henviser til fig. 14 og de efterfølgende skemaer. Skemaet er opbygget efter det princip, at først findes den trækkraft, der er til rådighed ved drivhjulene. Fra dette trækkes så de modstande, der optræder. I linie 2 indsættes 2 strømaftagere á 60 g, ligegyldigt om begge sæt sidder på maskinen, eller det ene sæt sidder på tenderen. I linie 3 findes trækkraften ved at gange adhæsionsvægten med gnidningskoefficienten, µ = 0,2. I linie 4 fratrækkes gnidningsmodstanden for strømaftagere, idet trykket ganges med µ = 0,2 og antallet 2. I linie 6 fratrækkes stigningsmodstanden for hele maskinen, dog uden en eventuel tender. De øvrige modstande-rullemodstande behandles nøjagtigt som de blev i fig. 8, nemlig som selvstændige vogne.

Ved valget af de efterfølgende eksempler har jeg forsøgt dels at illustrere skemaets brug ved valg af forskellige lokotyper, dels at sætte realistiske vægt på eksemplerne, uden ligefrem at have vejet bestemte modeller på anlægget. Af eksemplerne kan følgende retningslinier uddrages:
1) Adhæsionsvægten skal være så stor som muligt.
2) Løbebogier og tendere skal være så lette som muligt.
3) Så mange aksler som muligt bør være drivende.
4) Løbeakslernes lejring bør være så god som muligt.
Klik for at se >> fig. 15 >> fig. 16 >> fig. 17 >> fig. 18 >> fig. 19
Som afslutning på denne lange snak har jeg sammenlignet de forskellige loko fra eksemplerne med vognene fra de tidligere eksempler, således at lokoene er opført i de nederste rækker, medens vognene er anført i de fem sidste lodrette kolonner. I felterne er så anført, hvor mange vogne det kan forventes at lokoet kan starte med, når hele toget står i en kurve, der ligger på en stigning. Den sidste, lodrette kolonne er en tænkt vogn med en modstand så stor som gennemsnittet af de foregående fire.
Jeg synes selv, at tallene i fig. 20 ser ganske sandsynlige ud; men som tidligere sagt, jeg skal ikke give det udseende af, at denne udredning er dækkende for alle forhold, kun at de talværdier, det er muligt at finde ved at benytte den opstillede beregningsmetode ikke ligger så fjernt fra sandheden.
| Vogne | Fig. | 9 | 10 | 11 | 12 | Gennemsnit | ||
| Litra | Hbis 211 5 000 | Hbis 211 5 099 | AF 78 | AF 82 | ||||
| Rullemodstand [g] | 23 | 54 | 17 | 57 | 38 | |||
| Træk- kraft |
Fig. | Litra | Trækkraft [g] | Antal vogne pr. trækkraft | ||||
| 15 | F | 118 | 5 | 2 | 7 | 2 | 3 | |
| 16 | S | 260 | 11 | 5 | 15 | 4 | 7 | |
| 17 | P | 105 | 4 | 2 | 6 | 2 | 3 | |
| 18 | My 1101 | 461 | 20 | 8 | 27 | 8 | 12 | |
| 19 | My 1108 | 107 | 4 | 2 | 6 | 2 | 3 | |
Skulle nogen af de læsere, der har hængt ved så langt som hertil, have oplysninger der kan belyse emnet yderligere, eller have spørgsmål i samme anledning, hører jeg meget gerne fra dem, og skal forsøge at svare efter bedste evne.
Ændringer:
2008-03-15: Opdateret til HTML 4.01 Strict, enkelte fejlrettelser, figurer rescannet, fig. 20 omlagt til tabel.
2009-01-01: Typografi opdateret.